I feel like the guest who came to dinner. I was going to look at the STAR*D study as a counter-example of an NIMH Clinical Trial to those sponsored by industry, and I can’t seem to move on to the next place – over a hundred articles "full of sound and fury…" In my wanderings, I ran across an article that used the STAR*D dataset and actually had something interesting to say. In their introduction , they described the study, and I felt like I was learning what actually happened in Level I [citalopram treatment] for the first time.
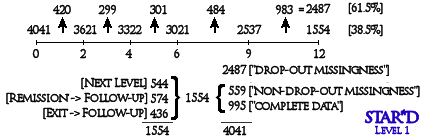
The current analyses focus on subjects going through the 12-week Level 1 treatment step of STAR*D, with depression severity repeatedly measured by a summed score from the 16-item Quick Inventory of Depressive Symptoms–Clinician Rated [QIDS-C, or QIDS for short] with a range of 0–27. The Level 1 visit schedule included baseline and Weeks 2, 4, 6, 9, and 12. Of the 4,041 subjects, 995 had complete data for all six occasions, 420 dropped out after the baseline, 299 dropped out after Week 2, 301 dropped out after Week 4, 484 dropped out after Week 6, and 983 dropped out after Week 9. In this way, 62% of the subjects had a dropout missing data pattern, 14% had nondropout intermittent missingness, and 25% had complete data for all six occasions. The coverage at baseline and Weeks 2, 4, 6, 9, and 12 was 1.00, .79, .69, .68, .57, and .39, respectively.
I drew it for us to look at:
4041 started and 62% of them dropped out along the way. Of the ones that stayed, 995 [25%] had all six values and 559 [14%] stuck with the program to the end, but had some missing data along the way. What happened is clear, unlike the STAR*D report in the AJP. Then …
STAR*D distinguished between three Level 1 endpoint categories of subjects: Subjects were moved to the next level if the medication was ineffective or not tolerated [35%], subjects were moved to follow-up if showing remission [37%], and subjects exited the study for unknown reasons [28%]. Here remission was defined as a Hamilton-D score of <7 and, if not available, a self-reported QIDS score of <5 (Hamilton-D was measured only at baseline and end of Level 1). The percentage of dropouts in the three Level 1 endpoint categories were 61% [next level], 35% [follow-up], and 95% [exit study].
… two thirds of the people who tried other treatments after Level 1 dropped out, a third of the Level 1 remitters in follow-up dropped out, and virtually all of the Level 1 non-remitters who didn’t choose to try a second treatment path dropped out. Here’s the abstract of the article:
Growth Modeling With Nonignorable Dropout: Alternative Analyses of the STAR*D Antidepressant Trial
Bengt Muthe´n, Tihomir Asparouhov, Aimee M. Hunter, Andrew F. Leuchter
Psychological Methods 2011, Vol. 16, No. 1, 17–33.
This article uses a general latent variable framework to study a series of models for nonignorable missingness due to dropout. Nonignorable missing data modeling acknowledges that missingness may depend not only on covariates and observed outcomes at previous time points as with the standard missing at random assumption, but also on latent variables such as values that would have been observed [missing outcomes], developmental trends [growth factors], and qualitatively different types of development [latent trajectory classes]. These alternative predictors of missing data can be explored in a general latent variable framework with the Mplus program. A flexible new model uses an extended pattern-mixture approach where missingness is a function of latent dropout classes in combination with growth mixture modeling. A new selection model not only allows an influence of the outcomes on missingness but allows this influence to vary across classes. Model selection is discussed. The missing data models are applied to longitudinal data from the Sequenced Treatment Alternatives to Relieve Depression [STAR*D] study, the largest antidepressant clinical trial in the United States to date. Despite the importance of this trial, STAR*D growth model analyses using nonignorable missing data techniques have not been explored until now. The STAR*D data are shown to feature distinct trajectory classes, including a low class corresponding to substantial improvement in depression, a minority class with a U-shaped curve corresponding to transient improvement, and a high class corresponding to no improvement. The analyses provide a new way to assess drug efficiency in the presence of dropout.
As you can see, it’s a technical article using computer modeling and a mathematics that I don’t [and never will] understand. In spite of the density of their analysis, I think there are some things we mere mortals can learn from their efforts. First, they took the very high drop-out rate in STAR*D seriously. They saw it as data, something to be understood. Recall this amazing statement from the official paper:
… this estimate assumes no dropouts, and it assumes that those who exited the study would have had the same remission rates as those who stayed in the protocol.
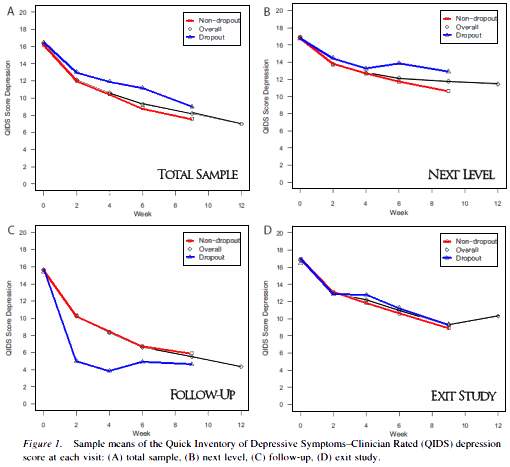
That from a study with a 62% drop-out rate in its opening gambit. In this article, the authors take on the second assumption as well. They displayed the Level 1 QIDS [Quick Inventory of Depression Symptoms] scores for the remitters who went to follow-up, the non-remitters who chose to exit the study to follow-up, and the people who chose to try another treatment at the next level. The blue lines are the means of the people who were going to drop out before the next period, and the red lines are the means of the people who were going to stay:
The remitters dropped out because they were remitting. The non-remitters dropped out because they weren’t. In other words, drop-outs weren’t random. Which brings up something else that proves these authors to be real scientists. They didn’t look at the missing data as a nuisance, they studied it – were curious about it. As the title of their paper says, they saw that data as "non-ignorable."
This article considers growth modeling of longitudinal data with missingness in the form of dropout that may be nonignorable. Nonignorable missing data modeling acknowledges that missingness may depend on not only covariates and observed outcomes at previous time points as with the standard missing-at-random (MAR) assumption customarily made in multivariate analysis software…
The MAR assumption of dropout as a function of the observed QIDS outcome is not necessarily fulfilled for subjects in any of the three Level 1 endpoint categories. Variables not measured or not included in the model, that is, latent variables, may affect missingness. Some subjects may leave Level 1 because of not tolerating the medication, unrelated to the level of depression. Some subjects may leave the study for unknown reasons… Modeling that explores possibly nonignorable missing data is therefore of interest in order to draw proper inference to the population of subjects entering Level 1.
Here’s the part we skip over because it looks like this:
Essentially, they begin to try a variety of models that don’t assume random drop-outs, considers the factors that predict the probability of drop-outs, considers the effect of the symptoms themselves, use complex multiclass mixed models that transcend the simple notions that people are either responders/remitters or not. Then they checked the fit against the data. Flash forward through the math/computer stuff I don’t understand. In the various modelings, there’s a class we haven’t thought much about, but it’s intuitively obvious once they say it. Here’s an example in one of those models:
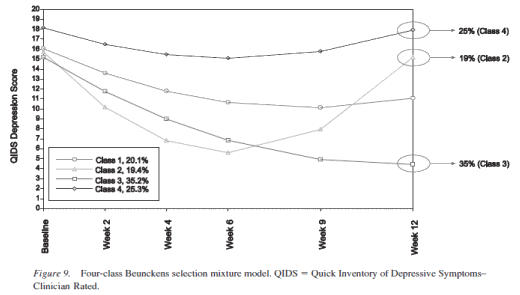
Look at Class 2. They call it the "U Class" – people who respond early, but then end up back where they started. And these authors find that a "U Class" makes the data make sense in multiple models, just differing in proportions among them. Why would I blog about a study with a mathematical analysis that I don’t really understand? Two reasons: First, every clinician whose ever prescribed an SSRI has seen such patients. Second, those patients were in STAR*D too. The authors had the raw data and parsed them out for us to see for ourselves:
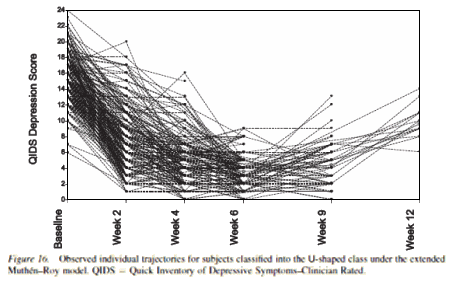
Notice that they respond/remit, then begin to relapse between 6 and 9 weeks and between 9 and 12 weeks [just like those drop-out numbers up top show them doing]. So our mathematicians propose that the group is heterogeneous in its response: a group of responders; a group of non-responders; and a third group that responds early then relapses – the "U Class." Their analysis explains drop-out rates as an integral part of the data – as something understandable.
Several things: This article is not ghost written. I’m sure of that.. So are you. If you read the whole thing, you’d see that they had a genuine encounter with the data generated by STAR*D. This article in a few paragraphs shows us the study with all of its drop-outs just as it happened. Then, instead of hiding the drop-out rate, they explained it. They do some complicated modeling mojo along the way, but at least I could follow what they were getting at. And finally they returned to STAR*D to show us what they were proposing using raw data.
I said it was refreshing because I left it with some decent questions. Were I a researcher, I’d be thinking about what it means for a long time and maybe generating thoughts about how to predict class responses in advance, or what it might mean about the SSRIs, or what these classes might represent, or about who is in the "U Class." In short, my curiosity was aroused. When I read the official STAR*D report and editorial, all I thought about was "what are they hiding?"; "what is their agenda?"; "when do they get to the science part?"; "what are their Pharma connections?"
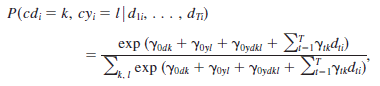
Sorry, the comment form is closed at this time.