While I haven’t thought about it very much, I made a move from the hardest of medical sciences to the softest without any transition. The first time around was in a lab with scintillation counters printing data to punch cards to feed into Fortran programs that cranked out ANOVA with p values. And then I was in the world of psychotherapy where there was little in the way of a control group [or for that matter – any groups], and validation was subjective at best – only clinical. There’s a gulf there that seems like it needs some of those connectomes Dr. Insel loves to talk about. 
But apparently I’m not the only person around with that kind of connectome problem. Many of my colleagues seem to obsess about clinical trials and their p values without addressing what matters – clinical relevance. So what! if a drug group in a clinical trial statistically separates from the placebo group if the people treated don’t even notice the difference. Large groups don’t come to our offices, individuals come. So the question is how to take those numbers that are generated in a clinical trial and turn them into something that really matters to the patients and doctors that inhabit those offices. Likely almost anyone reading this already knows what I’m about to say, but I’m about to say it anyway. So this is that post you might want to skip…
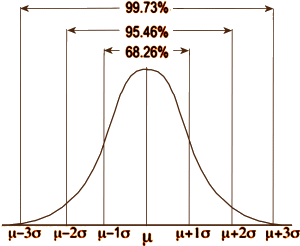Over there on the right is our old friend, Mr. Normal Distribution. If you take a large sample of almost anything, the values will look like this with the measurement variable across the bottom [abscissa] and the frequency of the values on the left axis [ordinate]. So you can describe a dataset that fits this distribution [most of them] with just three numbers: μ [the mean, average]; n [the number of observations]; and σ [the standard deviation, an index of how much variability there is within the data]. 95% of the values fall between two standard deviations on either side of the mean. That means that measurements outside those limits have only a 5% chance of belonging to this group – thus p < 0.05 [p as in probability]. 
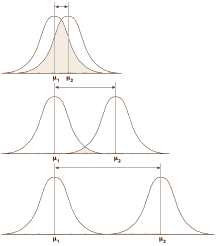In the examples on the left, all three might be statistically significant but looking at the p value won’t tell you anything about the likelihood it will be a property noticed by individual patients. It might be simple a chemical finding that’s imperceptible, or it might be a power-house. But p doesn’t tell you that. Regulatory bodies, like the Food and Drug Administration [FDA], were established to keep inactive patent medicines off the medical market, not to direct drug usage or attest to the magnitude of their effects. So the FDA insists on two well conducted Clinical Trials that demonstrate statistically significant differences between the drug and a placebo. The main task of the FDA Approval process is safety – what are the drug’s potential harms? Efficacy is a soft standard added on in 1962.
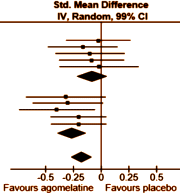There are no absolute standards for a meaningful Standardized Mean Difference. Cohen suggested 0.25 = weak; 0.50 = moderate; 0.75 = strong. But you could gather a bunch of statisticians and they could argue about that for the whole evening. The place where Effect Sizes are routinely used is in meta-analyses that compared multiple studies and/or multiple drugs. I guess you could say it’s a powerful relativity tool, often combined with a representation of the 95% Confidence Interval. In the example on the right from the article quoted above, the Standardized Mean Difference is on the Abscissa with the Confidence Intervals as the horizontal line [in this example, the 99% Confidence Intervals were used]. This is the format used in the Cochrane Systematic Reviews called a forest plot and it tells us a lot. The top 5 studies are unpublished Clinical Trials of agomelatine vs placebo. The weighted average is 0.08 in favor of agomelatine [which might as well be zero], and none are significant at the 1% level [the Confidence Interval line crosses zero]. The bottom 5 studies are published studies of agomelatine. The weighted average is 0.26 with only one significant at the 1% level. Overall, the weighted average Standardized Mean Difference is 0.18. In everyday language, a trivial effect with clear publication bias.
So why go through with all of this simplified statistical mumbo jumbo? It’s because these seasoned Cochrane meta-analizers take a very credible stab at translating their findings into the realm of clinical relevance in the colored paragraph above. Whether you use the Standardized Mean Difference of 0.18 evaluated by the values I quoted above, or the HAM-D Mean Difference of 1.5 HAM-D units as they did, these studies may be statistically significant at p < 0.05 [the published ones are], but they are able to conclude that it is not a clinically relevant difference, particularly when you look at the studies Servier neglected to let us see. So there’s my mythical connectome between the numeric part of my brain and the part that practices clinical medicine. Very satisfying.
So why don’t we see Effect Sizes plastered all over these Clinical Trials that have flooded our journals? They use the same data as the statistical calculations that are invariably prominently displayed. Would you publish them if your main goal was to sell agomelatine? Probably not because nobody would be very excited about either prescribing it or taking it. You’d display Effect Sizes and their Confidence Intervals if you wanted to give clinicians and patients as accurate as possible a notion of how effective the medication might be in relieving the targeted symptom – pending the later results of the reported responses in our offices where clinical medicine meets real live people in pain.
Alvan Feinstein at Yale came up with the term clinimetrics to underscore the difference between statistically significant differences and clinically meaningful differences. Number Needed to Treat (NNT) is a good example of a clinimetric index. Experimercial studies typically are overpowered with huge sample sizes to ensure statistical significance while lacking clinimetric significance.
From the letter referenced above by Dr. Carroll. A line to remember…
by BERNARD J. CARROLL
Am J Psychiatry 2004 161:759-759.
… The authors also failed to emphasize in the abstract (where most readers would notice it) that none of the functional or quality-of-life outcome measures favored sertraline over placebo. Something has changed in our conceptual paradigm when a drug can be described as “effective” for depression, but the patients do not confirm that their lives are any better with respect to vitality, social functioning, emotional role functioning, or mental health. Like the Cheshire cat’s smile, the only evidence that sertraline was there is the disembodied p value, grinning in statistical space, with no connection to clinical reality.
Mickey,
Thank you for the review, it has been many, many, many years. You are still teaching and we are still learning.
Frustrated many years ago I knew there was a better way to state drug effectiveness. I am a business person so I am interested in odds. Then someone showed me NNT. The clouds parted.
The doctor run web site: http://www.thennt.com/ addresses just this issue and covers some common drugs and test. The results are not always what those selling these items want to hear.
Every preventable death and every person in treatable pain is a tragedy. The problem is when we mandate or set population wide standards that will only help a few are we really solving the problem?
The drug and other companies in health will say yes, those subject to painful injections, surgery, or who knows what, with little or no discernable results may have a different opinion.
Steve Lucas
Steve,
A number of years ago, Merrill Goozner wrote an article about NNT. Wow! I may never had courses in statistics, but the article was a real eye-opener about who is really paying for what–and who benefits.
Please allow me to point out again: If drug companies were interested in debunking each others’ cooked research, they could easily do this on the basis of the analysis Dr. Mickey provided above.
But they do not and never will seriously critique each others’ research, because nobody wants to broach the gentleman’s agreement on the infomercial practices from which they all benefit.
History has already demonstrated that the competition of the free market is not a corrective for jimmied stats or unjustified conclusions in pharma-sponsored medical research.
On the matter of NNT, much depends on the clinical context… it’s not a case of one size fits all. In the acute treatment context the British NICE guideline of NNT less than 10 seems appropriate – though one really aims for NNTs in the range of 5 or below. That’s what we had with the early antidepressant drugs (NNT = 3) but not with the SSRIs (NNT = 9-11 or higher). Remember, NNT tells us how many patients we need to treat to obtain one prespecified outcome with active treatment over and above what we would expect to obtain with placebo treatment. When the clinical context shifts to preventing relapse of depressive episodes for 12 months after achieving remission, however, the NNT for both the old and the new antidepressant drug classes is 2-3.
In yet another clinical context, prevention of disease progression, we accept much higher NNTs. For instance, for the hard endpoint of preventing 1 death over 10 years by treating hypertension the NNT is somewhere between 23 and 81. But we do treat hypertension anyway, because it is supported by other benefits such as longer term survival and quality of life.
And then when we move to the context of screening for disease the NNTs increase by 2 orders of magnitude. To prevent one death from colon cancer over 5 years by screening for blood in the stool the number is 1374. For the same hard outcome of preventing one death from breast cancer over 5 years by mammography screening the number is 2451.
In all these cases a corresponding clinimetric measure called Number Needed to Harm (NNH) can also be estimated, and clinical decisions turn on the balance between NNT and NNH, along with cost-benefit analyses. And, as the clinical science evolves with new evidence, practice may change – witness the recent reappraisals of the value of routine mammography screening of low-risk patients.
As described by Dr Carroll, NNT/NNH is a very clinically useful number and I think provides a useful context for the particular intervention. I make my trainees calculate for every paper we read in out journal club as a way of contextualizing a treatment to the scale of an individual practitioner. The NNT to NNH difference can be very informative, just calculate for Abilify as antidepressant augmentation. I would add one clarification on Cohen d though, and that is the strength of the effect is the strength of the statistical effect not of the potency of the medication. A strong effect size means that on some infinite replications of the trial the same result will be obtained over and over while a weak effect size means that on replication an alternative finding of no difference will likely occur. It is an indirect measure of the impact of the treatment as one would expect a highly efficacious treatment to continue to result in statistically significant differences on multiple replications. It speaks more to the veracity of the finding than the potency of the medication.
Steve,
I’m not sure I understand this. Do you have a suggested reference? It’s topic I’d like to pursue…
Mickey
One problem in comparing efficacy of older antidepressants and the MAOIs (which I am fond of using in selected refractory patients) in particular to SSRI/SNRI studies is the changing definition of depression from 1960-present. It seems fairly obvious that the earlier studies dealt with a sicker population. Hence, greater response rates with newer drugs but also greater placebo response rates, which is the giveaway that these were a lot of self limited conditions that were going to get better anyway.
So I am not surprised that NNT for older drugs is a lot better. If you can manage side effects…
Great letter, Dr. Carrol, it was a joy to read. I’ll recommend it the next time I run into someone giving a study their blessing because of the sample size alone.
NNT is informative, but the number of people needed to be treated in order to save one life doesn’t have much to do with the odds that the medication will work for any particular person, which is exactly what’s being said here, of course. Most people, including myself, are weak in heuristics, but doctors should be able to explain the odds and put them in a context in which the patient can relate. Without honest studies with honest numbers, they can’t effectively do that, of course. I suspect that a whole lot of clinicians could brush up on statistics and methodology.
Even if a medication only works for 1 out of a 1000 people, it might really work for that one person when nothing else helps. And if a med doesn’t work, it doesn’t work— it’s important to let patients know that that’s not a failing on their par, especially when they find the effects unacceptable.
What’s most important, I think, is for doctors to explain from the outset that it’s always a gamble, and to give the patient a clear and accurate picture of the possible risks versus possible benefits and make it clear that finding the right med or discontinuing a med may require time, trial, and error. The patient should know that they’re taking risks and— given sufficient information— should be able to share the responsibilities for that risk.
A pharmaceutical outfit for geriatric care recommends that all symptoms a person suffers after starting a new medication should be assumed to be caused by the medication until proven otherwise. I think that should apply to everyone.
The lack of truly informed consent in medicine these days is a terrible violation of trust. One of my stepmother’s sister had a spot show up on a mammogram last year. All the women on that side of my family went full-metal jacket on the pink ribbons and positive thinking. I bit my tongue, and wished her well, but it made me feel queasy. The doctors removed a lymph node and then told her that they got it all and that she wouldn’t require any more treatment, which was good news; but I cannot trust the way the medical field is treating breast cancer and have to wonder if the surgery was necessary at all. I wish the women who thought they were working on behalf of women’s health had been convinced otherwise about the radiation threat from mammograms. It’s still frowned upon and considered stupid or careless to forgo mammograms. That is a threat to women’s health. It’s very frustrating and reminds me of the hysterectomy mania in the eighties. The same seems to be true about a lot of prostate cancer, too.
I think for most people, questioning their doctors is unacceptable or they’re too timid to do so. I have no such problem with that, but I do feel like I have to justify some of my decisions to my GP because I like her and respect her. My neurologist is an intern, and I’m going to teach him a thing or two about listening and not scheduling MRIs routinely and unnecessarily. There are too many vets waiting in line with TBIs.
Slowly, but surely, I think the problems that start with the pharmaceutical companies and ends with them are being challenged. I’m rooting for you guys.
All good points, Wiley. Glad you appreciated the letter.
RE: cohen’s d and statistical significance @Steve @Mickey
Both p values and confidence intervals are part of Fisher’s Null Hypothesis Significance Test. They calculate the likelihood of getting a result given a hypothetical infinite sampling distribution of equivalent tests. It’s important to note that the hypothetical tests which make up the sampling distribution have to be equivalent (i.e. in both sample size and experimental context) because that’s the reason we can’t compare p values between one study and another.
As I understand, this is not the case for Cohens d. Cohen’s d is simply (as Mickey suggests) the standardised mean difference between groups (or, to put it another way, the mean group difference expressed in terms of the standard deviation). It doesn’t depend on a hypothetical sampling distribution because it is entirely independent of statistical significance. It’s for this reason that it can be used to compare the effect size (or mean difference) between studies. It’s also the reason that a study can have a large mean difference between groups (e.g. a large effect size) while failing to reach statistically significance. Alternatively, and this is the case Mickey outlined above, a study can be statistically significant without having a meaningful difference between groups (e.g. a low effect size).
The problem with the NNT/NNH method for assessing clinical relevance is that you are always dividing “apples” by “oranges”, and due to the many different possible harms of each treatment, many different ratios can usually be calculated. For example, with SSRIs you can choose to calculate the NNH for nausea on initiation, and you would get a very low number, and hence an unfavourable NNT/NNH, or you could choose GI bleeding (high NNH), and then get a favourable ratio.
Gad Mayer is quite right in what he says about apples and oranges when appraising NNT in relation to NNH. That’s why I didn’t state a formula for comparing them. Sometimes one can compare apples to apples, however, as in NNT for preventing suicide with antidepressant drugs versus NNH in provoking suicides with the same drugs. In other situations, as he describes, we do our best to give ad hoc weights to the benefits and the harms – we use clinical judgment.
What are the stats for “NNT for preventing suicide with antidepressant drugs versus NNH in provoking suicides with the same drugs”?
Alto, if you go to the link I included then you may be able to link from there to the text of my 2004 letter in JAMA on this subject. My estimates suggested that there is equipoise between NNT and NNH – in other words it’s a wash as far as completed suicides are concerned. Both numbers were over 500. Here is the letter:
Letters | December 1, 2004
Adolescents With Depression
Bernard J. Carroll, MB, BS, PhD
[+] Author Affiliations
JAMA. 2004;292(21):2577-2579. doi:10.1001/jama.292.21.2578-a.
To the Editor: In interpreting the TADS results,1 the central issue is the benefit-to-risk ratio, which can be determined by considering the number needed to treat (NNT), the number needed to harm (NNH), and the number needed to prevent.2 In this study, a categorical positive response was achieved in 71.0% of participants treated with fluoxetine in combination with CBT; in 60.6% with fluoxetine alone; in 43.2% with CBT alone; and in 34.8% with placebo. Based on these outcomes, the NNT is 3.9 for fluoxetine alone compared with placebo and 3.7 for drug vs no drug. I believe that these represent low NNTs (high benefit) that are clinically meaningful.
The TADS Team reported suicide-related adverse events in 6.9% of children taking fluoxetine and in 4.0% of children who did not take fluoxetine; this corresponds to a NNH of 34. Likewise, TADS reported suicide attempts in 6 (2.78%) of 216 adolescents taking fluoxetine and in 1 (0.45%) of 223 adolescents not taking fluoxetine. The corresponding NNH is 43. The NNT is far more salient than either NNH.
There were no completed suicides in the TADS trial. Nevertheless, extrapolating from epidemiological data that indicate 8% of reported suicide attempts overall are lethal,3 the estimated NNH with an outcome of completed suicide would be 535. Balancing any risk of drug-attributable suicide is the prevention of disease-attributable suicide in patients who receive the drug. Using a conservative lifetime case-fatality rate estimate of 2.2% among outpatients diagnosed as having MDD,4 and allocating 30% of this risk to the adolescent years,5 a completed suicide rate of 0.66% would be expected. When the TADS-observed NNT of 3.7 is applied to these estimates, the number needed to prevent 1 suicide is 560. Thus, there is suggestive evidence of equipoise between the therapeutic outcome of preventing suicide and any potential drug-related provocation of suicide among adolescents treated for MDD with fluoxetine. Overall, these estimates of absolute risk support the conclusion that favorable benefit-to-risk ratios exist for treatment with fluoxetine in adolescents with MDD.1
References
1
Treatment for Adolescents With Depression Study (TADS) Team. Fluoxetine, cognitive-behavioral therapy, and their combination for adolescents with depression: Treatment for Adolescents With Depression Study (TADS) randomized controlled trial. JAMA. 2004;292:807-820
PubMed | Link to Article
2
Laupacis A, Sackett DL, Roberts RS. An assessment of clinically useful measures of the consequences of treatment. N Engl J Med. 1988;318:1728-1733
PubMed | Link to Article
3
Spicer RS, Miller TR. Suicide acts in 8 states: incidence and case fatality rates by demographics and method. Am J Public Health. 2000;90:1885-1891
PubMed | Link to Article
4
Bostwick JM, Pankratz VS. Affective disorders and suicide risk: a reexamination. Am J Psychiatry. 2000;157:1925-1932
PubMed | Link to Article
5
Goodwin FK, Jamison KR. Manic-Depressive Illness. New York, NY: Oxford University Press; 1990
Great, trying to bring down the suicide rate with meds on a grand scale is essentially pushing on a string…doesn’t discount other benefits of treatment…
I’d like to make two observations about the TADS study discussed above. First, the response rates and NNT figures in Dr. Carroll’s letter were based on outcomes at week 12, which favoured combined treatment and fluoxetine. From 36 weeks on through 12-month follow-up, response rates were equivalent across CBT, fluoxetine, and their combination. Second, as Whitaker noted in 2012 (http://www.madinamerica.com/2012/02/the-real-suicide-data-from-the-tads-study-comes-to-light/), the “real” TADS suicide data were not included in the original efficacy report and were essentially unearthed by bloggers who located them in a relatively obscure 2009 publication. These data show a much higher prevalence of suicidal events (combined across 12 weeks and 12 to 36 weeks) in the flouxetine groups (16.7%) than the CBT group (3.6%). These data are provided here in response to Altostrata’s query regarding the NNT and NNH figures for antidepressants.
Brett,
see also significant I… and significant II…
Mickey, fantastic analysis! I will bookmark it for future reference.
Sure, Brett, and I weighed in when the Whitaker update surfaced. The obfuscation has been so thick that even today we probably still don’t have all the data we need.
Thank you, Dr. Carroll. NNT and NNH surely would have been a more constructive way to analyze the findings of TADS (and all other drug studies), even with all the flaws in the data, which render any conclusions based on TADS highly questionable.
As akathisia, an adverse effect of antidepressants, is implicated in drug-induced suicidality, I offer this blog and its comments http://akathisiainfo.wordpress.com/2013/08/13/my-akathisia-experience/#comments