1 Boring Old Man

Psychiatry’s Mind-Brain Problem

New York Times – Opinion

By GEORGE MAKARI

NOV. 11, 2015

…

Unfortunately, Dr. Kane’s study arrives alongside a troubling new reality. His project was made possible by funding from the National Institute of Mental Health before it implemented a controversial requirement: Since 2014, in order to receive the institute’s support, clinical researchers must explicitly focus on a target such as a biomarker or neural circuit. It is hard to imagine how Dr. Kane’s study [or one like it] would get funding today, since it does not do this. In fact, psychiatry at present has yet to adequately identify any specific biomarkers or circuits for its major illnesses.

Critics worry that this new stipulation will limit clinical studies and foster what has been all too familiar in psychiatry — unwarranted speculation aimed at prematurely reducing many layers of intersecting causality to one. If so, the institute will become the latest in a long, unhappy line of those who pressed for a simple solution to the Janus-faced problems of mind-brain illness. In the meantime, Dr. Kane’s study provides pragmatic clinicians with strong new evidence for an old idea: Individuals with mental illness should be fully engaged as beings whose rich psyches and ever-present social worlds are just as real as their brains.

Five years ago, the NIMH launched a big project to transform diagnosis. But did we have the analytical firepower to do that? No. If anybody has it, companies like IBM, Apple or Google do – those kinds of high-powered tech engines…

Kudos to Tom Jefferson for drafting our consensus letter to the presidential candidates published today in the British Medical Journal. I feel honored to be included in this list of heavyweights. Some may think that such gestures are ineffective, but I disagree. We’ve had years of silence and the results speak for themselves. Now people are speaking out, there’s movement – actually fairly rapid movement for the usual pace of things in medicine and science.

A university and clinical trial investigators must release data to a citizen-scientist patient, according to a landmark decision in the UK. But the decision could still be overturned if the University and investigators appeal. The scientific community needs the decision to be upheld. I’ll argue that it’s unwise for any appeal to be made. The reasons for withholding the data in the first place were archaic. Overturning of the decision would set a bad precedent and would remove another tooth from almost toothless requirements for data sharing.

We didn’t need Francis Collins, Director of National Institutes of Health to tell us what we already knew, the scientific and biomedical literature is untrustworthy.

And there is the new report from the UK Academy of Medical Sciences, Reproducibility and reliability of biomedical research: improving research practice.

There has been a growing unease about the reproducibility of much biomedical research, with failures to replicate findings noted in high-profile scientific journals, as well as in the general and scientific media. Lack of reproducibility hinders scientific progress and translation, and threatens the reputation of biomedical science.

Among the report’s recommendations:

• Journals mandating that the data underlying findings are made available in a timely manner. This is already required by certain publishers such as the Public Library of Science (PLOS) and it was agreed by many participants that it should become more common practice.
• Funders requiring that data be released in a timely fashion. Many funding agencies require that data generated with their funding be made available to the scientific community in a timely and responsible manner

A consensus has been reached: The crisis in the trustworthiness of science can be only overcome only if scientific data are routinely available for reanalysis. Independent replication of socially significant findings is often unfeasible, and unnecessary if original data are fully available for inspection.

Numerous governmental funding agencies and regulatory bodies are endorsing routine data sharing.

The UK Medical Research Council (MRC) 2011 policy on data sharing and preservation  has endorsed principles laid out by the Research Councils UK including:

Publicly funded research data are a public good, produced in the public interest, which should be made openly available with as few restrictions as possible in a timely and responsible manner. To enable research data to be discoverable and effectively re-used by others, sufficient metadata should be recorded and made openly available to enable other researchers to understand the research and re-use potential of the data. Published results should always include information on how to access the supporting data.

The Wellcome Trust Policy On Data Management and Sharing opens with:

The Wellcome Trust is committed to ensuring that the outputs of the research it funds, including research data, are managed and used in ways that maximise public benefit. Making research data widely available to the research community in a timely and responsible manner ensures that these data can be verified, built upon and used to advance knowledge and its application to generate improvements in health.

The Cochrane Collaboration has weighed in that there should be ready access to all clinical trial data:

Summary results for all protocol-specified outcomes, with analyses based on all participants, to become publicly available free of charge and in easily accessible electronic formats within 12 months after completion of planned collection of trial data; Raw, anonymised, individual participant data to be made available free of charge; with appropriate safeguards to ensure ethical and scientific integrity and standards, and to protect participant privacy (for example through a central repository, and accompanied by suitably detailed explanation).

Many similar statements can be found on the web. I’m unaware of credible counterarguments gaining wide acceptance. Yet, endorsements of routine sharing of data are only a promissory reform and depend on enforcement that has been spotty, at best. Those of us who request data from previously published clinical trials quickly realize that requirements for sharing data have no teeth. In light of that, scientists need to watch closely whether a landmark decision concerning sharing of data from a publicly funded trial is appealed and overturned…

He had always worked Construction, but when the housing market crashed, so did his livelihood. He couldn’t find work anywhere. His [sort of] wife was out of work as well. He got depressed and was started on Paxil 10 mg by a nurse practitioner. When it looked like he was going to lose his house, he went into the breaking and entering business for the first time in his life. After some early successes, he got caught in the act and found himself with no [sort of] wife, no house, and a five year prison sentence. I asked how the Paxil dose had gone from 10 to 60 milligrams. He asked me if I’d been to prison [first time I’ve ever been asked that]. But what he wanted to explain to me was how boring prison life can be and wondered if I already knew.

He said, "It’s like a grammar school playground. A bunch of guys with nothing to do except watch t.v., eat, and get in fights with each other. When you get in a fight, you end up on solitary for a few days. And I got really depressed in solitary so the doc increased my meds." That happened several times, and up went the medication dose. I asked if they gave him medications on solitary, but that was what he’d already figured out on his own – that it was withdrawal symptoms. "But by the time I figured it out, I was on 60 —-ing milligrams." The Remeron had been started because of insomnia, something he had never had before. His description of the withdrawal symptoms was classic, down to the brain zaps [for which he had a more colorful but less printable name]. He had tried to come down on the Paxil dose, but invariably got the symptoms late in the day and so he took the skipped pills. He would squirrel away a half pill here and there to build a "stash" in case of getting sent to solitary, and he had definitely learned to avoid fights. He was terrified that he wouldn’t be able to get the medication. The withdrawal symptoms were that bad. And he was convinced that he’d never sleep again without the Remeron.

He had already given a few hints along the way about how to proceed. He was on two drugs with withdrawal syndrome possibilities, one he knew about – Paxil. So Paxil seemed the place to start. His own attempts failed at "the end of the day." With the short acting drugs, people taking them only once a day often get evening symptoms and I even wondered if that was part of why the dose was so high [and maybe even wondered if that had something to do with the Remeron addition]. Something I’ve learned is that if one comes on too strong with the tapering meme, the patients get scared go elsewhere to someone who will just write the refills. So I suggested that the first order of business was to get him to a twice daily Paxil dosing. Move a half pill to the afternoon every week or two. When I explained why, he liked to idea. Once we got to a twice daily dose [30 mg twice a day], we could start a taper with  less fear of evening withdrawal symptoms. And if half a pill doesn’t work, I told him to try moving by quarters. But the real point is that he seemed to be on-board once he felt comfortable I wasn’t going to "cut him off."

He seems pleased as punch to be out of prison and I doubt he’ll ever go back [even as I wrote that, I remembered that my track record predicting criminality has not been stellar]. But I’d bet the house that his illness started as situational and is now iatrogenic [caused by his medications]. I know nothing about SSRI being associated with non-violent crime, but who knows if that Paxil had something to do with his later life new profession?

^{O! be some other name:
What’s in a name? that which we call a rose
By any other name would smell as sweet;
So Romeo would, were he not Romeo call’d,
Retain that dear perfection which he owes
Without that title.}

Richard Lehman’s journal review

BMJ

9 November 2015

Disingenuous denial

JAMA. 2015 314:1791. “Confluence, Not Conflict of Interest” now appears in print, and leads me to break my rule and comment on this article a second time, because I think it marks a low point for JAMA. It aligns the journal with the disingenuous deniers who pretend that conflicts of interest don’t arise when authors and investigators write about work that they have a vested interest in promoting. It joins together JAMA with the NEJM which took a similar stance in a series of opinion papers earlier this year. This is a sort of Republican Tea Party of the soul, where you know you are saying something false and daring people to contradict you, knowing that their very engagement is a form of legitimation. And besides, you have power over them and they don’t over you. Blake called this place Ulro, and it leads to nothing but harm and barrenness — for those involved as well as for everyone else. But it is perfectly possible to get out of Ulro and build a better world.

Given the broad array of stakeholders, the diversity of approaches, and the concern that such policies might restrain innovation and delay translation of basic discoveries to clinical benefit, the Institute for Translational Medicine and Therapeutics at the University of Pennsylvania recently convened an international meeting on conflict of interest…

UPenn Looks The Other Way At Ghostwriting

Pharmalot

By Ed Silverman

March 1st, 2012

The University of Pennsylvania has denied allegations made by one of its professors that several other academics – including his department chair – allowed their names to be added to a medical journal manuscript, but gave control of the contents to GlaxoSmithKline, according to his attorney. The study, which was funded by the drugmaker and the National Institutes of Health, looked at the impact of the Paxil antidepressant on patients with bipolar disorder.

At the same time, the university has acknowledged a claim by the professor, Jay Amsterdam, that the 2001 study was ghostwritten by Scientific Therapeutics Information, his attorney tells us. However, he says the university is not planning on taking any action in connection with the ghostwriting. The study, which was published by the American Journal of Psychiatry [see here], did not mention that STI played any role.

“They said his allegations were not meritorius, although they did find that the publication at issue was ghostwritten,” says Bijan Esfandiari, the attorney, citing a letter and other documents he received from the university. “They acknowledged that a marketing firm was involved in drafting, and everything associated with, the issue. But in response to our complaint, they said that, at the time these events took place, which was between 1998 and 2001, ghostwriting was standard practice and everyone was doing this, so therefore, we’re not going to punish any individuals”…

While there was, indeed, a lot of corruption in the years around the turn of the century, to dismiss it with something tanamount to "but there was a lot of that going around" as if it were a fad or a pesky virus hardly rises to any reasonable medical or academic standard. It’s an argument as lame as "… such policies might restrain innovation and delay translation of basic discoveries to clinical benefit." Medicine arose in ancient history and survived for centuries not based on powerful scientific advances. Those advances are only in their second century. Medicine prevailed because it was among the few professions that was able to adhere to a consistent and enduring ethical stance. A resistance to outside Conflicts of Interest has been an implied element of that ethic throughout our history. Arguments such as those expressed in this JAMA viewpoint article simply have no place in our tradition or our literature. And to have these recent articles actually advocating for conflicted authorship in our two major journals [NEJM: Revisiting the Commercial–Academic Interface, JAMA: Confluence, Not Conflict of Interest] is cause for alarm…

FACING THE UNRELIABILITY OF CLINICAL TRIALS LITERATURE

by Tom Jefferson

Drug and Therapeutics Bulletin of Navarre, Spain. 2015 23[2]:1-11.

[full text on-line]

Journal publications of randomised controlled trials [“literature”] have so far formed the basis for evidence of the effects of pharmaceuticals and biologics. In the last decade, progressively accumulating evidence has shown that literature is affected by reporting bias with evident implications for the reliability of any decision based on literature or its derivatives such as research synthesis. Instead of trying to reform the fields of research, industry, government, regulation and publishing, I propose basing public health decisions and reimbursement of any important intervention on independent trials and studies following the model pioneered by the mario negri Institute of Pharmacological research.

^{This is just some fluff. After all this time looking at the industry-funded clinical trials [RCTs], I’ve learned a few tricks for spotting the mechanics of deceit being used, but I realize that I need to say a bit about the basic science of RCTs before attempting to catalog things to look for. Data Transparency is likely coming, but very slowly. And even with the data, it takes a while to reanalyze suspicious studies – so to these more indirect methods. I expect there will be a few more of these posts along the way – coming mostly on cold rainy week-end days like today when there’s not much else going on. If you’re not a numbers type, just skip this post. But if you’re someone who wants to contribute to the methodology of vetting these RCTs, email me at 1boringoldman@gmail.com. Examples appreciated. It’s something any critical reader needs to know how to do these days…}

The word sta·tis·tics is derived from the word state, originally referring to the affairs of state. With usage, it has come to mean general facts about a group or collection and the techniques used to compare groups. In statistical testing, we assume groups are not different [the null hypothesis], then calculate the probability of that assumption. If it’s less than some value called alpha [0.05], we reject the null hypothesis and assume the groups are significantly different.

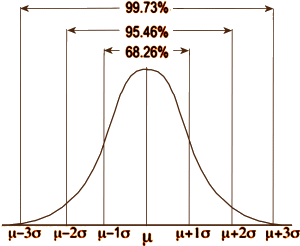In statistical testing, assumptions abound. For continuous variables, we assume that the data follow a normal distribution, so we can simplify the dataset into just three numbers: the mean [μ], the standard deviation [σ], and the number of subjects [n]. In an RCT, with just those numbers for the placebo group and the drug group, we can calculate the needed probability. In the normal distribution, all the items between two standard deviations on either side of the mean make up 95% of the sample. Values outside those limits make up only 5% of the sample. In doing statistical testing for the difference between two groups [assuming for the moment an equal σ and n], when the probability of the null hypothesis is 0.05 or less [p < 0.05], we feel confident that the groups are significantly different. But that only tells us that the groups are different – not how different.

In this simple two group example, calculating the p value depends on having the means [μ₁ and μ₂], the standard deviations [σ₁ and σ₂], and the two sample sizes [n₁ and n₂]. And this is about as far as they got in my medical school version of a statistics course in the dark ages called the 60s [only scratching the surface of the field]. So those of us doing research had to add some other degrees. They do a better teaching job in these modern times [with computers to do the heavy number crunching instead of the calculators that shook the table and sounded like Gatling guns]. And with the increased computer power came much more sophisticated statistical testing allowing the evaluation of many more factors in the models.

This is a case where one wonders if the technological advances have been all that helpful. In the past, medications were evaluated on clinical grounds. The efficacy scale was simple. It had it doesn’t work, it sometimes works, and it works – a scale suited to an effective medications. With the modern clinical trials, much smaller differences are the rule – sometimes in the range of absurdity. So, as most people know in the abstract, a p < 0.05 doesn’t necessarily denote clinical significance. It may mean absolutely nothing or conversely something of real value. But in spite of that knowledge, our eyes are invariably drawn to the ubiquitous p value like a magnet.

One attempt to get at a more relevant index of efficacy is to standardize the magnitude of the difference between the means of the two samples in some way – for example Cohen’s d [a way to compute the strength of the effect]. It’s the difference in the means expressed as a percent of the pooled standard deviation. Back to assuming an equal σ and n in the two groups, it would be:

d = (μ₁ – μ₂) ÷ σ

While there’s no strong standard for d like there is for p, the general gist of things is that: d = 0.250 [25%] is weak, d = 0.50 [50%] is moderate, and d = 0.75 [75%] is strong. Note: for groups of unequal size or distribution, the pooled σ is:

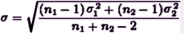
This graphic makes this point better, and gets around to why I’m writing this:

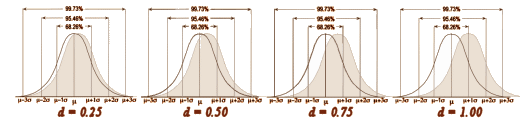
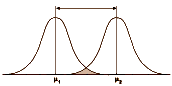Even a strong  Cohen’s d isn’t a huge separation – plenty of overlap still in the picture. So when you’re looking at Effect Sizes, don’t think it looks like the figure on the left [d = 4]. You’re usually still back in the land of sometimes when you’re looking at these Effect Sizes in a Clinical Trial report in a journal article.

Another point. You may have noticed that you need μ, σ, and n to calculate statistical significance, but only μ and σ to calculate Cohen’s d. The strength of effect is independent of the sample size. You can figure out how these thing relate to each other. With a drug that has a moderate effect [eg d = 0.50] you need only a small sample size to achieve statistical significance [even less if it’s strong]. But with a weak effect [d = 0.250], you need to have a whole lot more subjects in your study. Again, assuming two groups with equal size and distribution, the relationship looks like this:

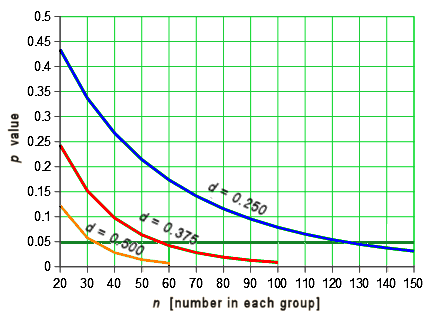
While these are the nuts and bolts of how one does Power Analysis when planning a clinical trial to figure out the needed sample size, that’s not why this graph is here. Most RCTs have p values listed, but many don’t have any version of the Effect Size [Cohen’s d, Odds Ratio, NNT, etc], probably because they’re weak sisters. So one thing to look for is that they have very large sample sizes. It’s in order to get that magic p < 0.05 they’re looking for to legitimize a weak effect. When the Effect Size is missing, you often have enough information to calculate it using the formulas above. Note: It’s common to have the Standard Error [se   or   sem] rather than the Standard Deviation [sd   or   σ]. But it’s easily converted using the formula:

se = σ ÷ √n    or    σ = se × √n

Brain expert: Why I jumped ship to Google

Silicon Valley offers a fresh way to tackle conditions such as schizophrenia says US mental-health expert Thomas Insel

The New Scientist

By Sally Adee

Nov 4, 2015

Why did you leave the National Institute of Mental Health to work for Google?

I have to confess that after giving heart and soul to mental-health problems over the last 13 years working in government, I have not seen any improvement for either morbidity or mortality for serious mental illness – so I’m ready to try a different approach. If it means using the tools available in the private sector, let’s go for it.

Are you saying Google is a better place to do mental-health research than the NIMH?

I wouldn’t quite put it that way, but I don’t think complicated problems like early detection of psychosis or finding ways to get more people with depression into optimal care are ever going to be solved solely by government or the private sector, or through philanthropy. Five years ago, the NIMH launched a big project to transform diagnosis. But did we have the analytical firepower to do that? No. If anybody has it, companies like IBM, Apple or Google do – those kinds of high-powered tech engines…

I was raised in a different research environment in my Internal Medicine days in Memphis Tennessee than I’ve seen in these years of research in Psychiatry. Memphis is in the upper reaches of the Mississippi. West Memphis Arkansas was once the Malaria capital of the US – the point being Mosquitoes. And where there are Mosquitoes, kids get Impetigo [a skin super-infection with Streptococci]. So we saw more Glomerulonephritis and Rheumatic Fever in kids and the chronic deadly versions in adults than anywhere. These are post-streptococcal diseases [once endemic but now rare]. The hemoglobinopathies like Sickle Cell disease were also prevalent in our area. So a lot of our researchers were Streptococcologists and Hematologists. The point is that research often starts with observations, like these epidemiological findings. The researchers flock and make other observations with clinical immersion.

Another example: My mentor had noticed some odd inclusions in electron micrographs of the capillaries of Lupus patients. We started a study doing electron microscopy of capillaries in Lupus, and the controls were other patients with non-Lupus connective tissue disorders. The study was a great success. The inclusions turned out to be insignificant artifacts, but what he found was that the patients with Scleroderma [in the control group] had a dramatic decrease in capillary density. That was a significant finding, but hardly the point of the study – an observation along the way. The classic example is the discovery of Penicillin. Alexander Fleming, a veteran of WWI, was involved in looking for antimicrobial agents, having seen so much sepsis in that war. He sure wasn’t studying dirty petri dishes. But when he saw a bacteria-free ring around a mold in a dirty petri dish, he knew what he was looking at – an observation along the way.

Insel’s and Hyman’s NIMH was built aiming for results. Translational research, meaning something that could race from bench to bedside. Focused research, meaning that one looked at what the higher-ups wanted and made up a proposal to fit. No career researcher grants – locating people with "the knack" and supporting them to follow their noses [eliminating the explorer class]. Insel’s NIMH was big on technology [like his comments above]. So the ordinate axis of his grand clinical neuroscience plan was literally technologies:

Here, he’s blaming the failure of his RDoC on inadequate technology [I think it’s more likely just a lousy idea myself]. So we have technology driven projects. He may be closer to the mark with identifying pre-psychotic states, but if he is, it’s a lucky guess without confirmation so far – exploratory. But I hold my point. He starts with the desired end rather than where we are. And that’s what his NIMH has produced – flat predictable results. The recent RAISE study is an example. Pay a lot of attention to initial episode psychotic patients and it helps. The earlier you start, the better the outcome. I knew that already. So did you.

As in love as he is with academic/industry partnerships, he has ended up with an NIMH that has done a lot of PHARMA’s work for them and colluded, if even unwittingly, with the rise of an academic/pharmaceutical complex the likes of which we’ve never seen; in a specialty [psychiatry] that we would’ve never dreamed might go down that path; achieving pockets of corruption beyond our previous imagination. And to my knowledge, Insel has never even mentioned any of that.

• Lurasidone in the treatment of schizophrenia: a randomized, double-blind, placebo- and olanzapine-controlled study.
  by Meltzer HY, Cucchiaro J, Silva R, Ogasa M, Phillips D, Xu J, Kalali AH, Schweizer E, Pikalov A, and Loebel A.
  American Journal of Psychiatry. 2011 168(9):957-67.
• Lurasidone Monotherapy in the Treatment of Bipolar I Depression: A Randomized, Double-Blind, Placebo-Controlled Study
  by Antony Loebel, M.D. Josephine Cucchiaro, Ph.D. Robert Silva, Ph.D. Hans Kroger, M.P.H., M.S. Jay Hsu, Ph.D. Kaushik Sarma, M.D. Gary Sachs, M.D.
  American Journal of Psychiatry. 2014 171:160–168.
• Lurasidone as Adjunctive Therapy With Lithium or Valproate for the Treatment of Bipolar I Depression: A Randomized, Double-Blind, Placebo-Controlled Study
  by Antony Loebel, M.D. Josephine Cucchiaro, Ph.D. Robert Silva, Ph.D. Hans Kroger, M.P.H., M.S. Kaushik Sarma, M.D. Jane Xu, Ph.D. Joseph R. Calabrese, M.D.
  American Journal of Psychiatry. 2014 171:169–177.
• Efficacy and Safety of Brexpiprazole for the Treatment of Acute Schizophrenia: A 6-Week Randomized, Double-Blind, Placebo-Controlled Trial
  by Correll CU, Skuban A, Ouyang J, Hobart M, Pfister S, McQuade RD, Nyilas M, Carson WH, Sanchez R, and Eriksson H.
  American Journal of Psychiatry. 2015 172[9]:820-821.
• A multicenter, randomized, double-blind, controlled phase 3 trial of fixed-dose brexpiprazole for the treatment of adults with acute schizophrenia.
  by Kane JM, Skuban, Ouyang, Hobart, Pfister, McQuade, Nyilas, Carson, Sanchez, and Eriksson.
  Schizophrenia Research. 2015 164[1-3]:127-35.

I’ve been thinking about this ever since we wrote the RIAT 329 article. It felt odd to me that our group was writing about subjects we’ve never seen. But then it occurred to me that it’s the standard in a lot of the Contract Research Organization managed studies. The other thing that occurred to me over and over was that our group had no direct contact with any of the twenty-two authors of the original Paxil Study 329 – only with the sponsoring pharmaceutical company. And reading through the Clinical Study Report, it was obviously written by and analyzed by the sponsor. Even the professional ghost-writer worked off of some version of a summary document prepared by the sponsor. I would suspect that the same is true about the articles above. I guess we’re just so used to the primacy of the sponsors, in spite of the fact that we anachronistically still refer to these articles as "Kane et al" or "Keller et al" [how quaint!].

It just doesn’t seem to register anymore that this class of articles reporting clinical trials is published in academic journals, but it has no real connection to anything "academic." I’ve referred to the authors highlighted in red as "tickets," as if their function is to certify admission to the journals. I recently suggested facetiously in maybe nowhere… that…

It would be fine with me if there were a specific journal for that kind of paper – the Journal of Industry Financed Reviews and Clinical Trials in Psychopharmacology… If the peer reviewed academic journals absolutely need the revenue, they could at least put these articles in a labeled, dedicated section of their publications with a heading [I suggest Industry Financed Reviews and Clinical Trials in Psychopharmacology].