1 Boring Old Man

I don’t much like questionnaires. But if required, I prefer yes/no or one word answer questions. And I’ve never designed a questionnaire [before today]. But as I was thinking about post-approval monitoring, I decided I’d give it a shot. I was thinking about what information you might gather post approval in help seeking patients taking the drug. You wouldn’t much care about controls, or statistical medicinal properties. You’d want to know what a clinician would want to know – is it helping? any problems? And how would one gather such information?

There are two points of contact – the drug store and the office/clinic. The pharmaceutical companies have had success  with the former. Their drug reps know what doctors are prescribing to inform their sales calls. If a patient filled out a brief questionnaire at the drug store, I think they’d have to give consent to have that information passed on if it were by patient. I don’t know if that would apply by drug alone. But how long the patient took the medication has traditionally been an useful parameter to consider.

"What about the waiting room questionnaires? I’d much rather they ask about the medications the patient is on than being used to screen for depression. It’s really the ongoing data after a drug is in use that clinicians need anyway – more important than the RCT that gets things started…"

I’ll be the first to admit that I’ve been pretty muddled these last several months – since, oh say, around 10:00 PM on November 8th, 2016 to be more precise. I’ve tried out any number of defense mechanisms to tell myself that I’m doing just fine. But to be honest, this election sort of took the wind out of my sails and I expect others of you might have experienced something similar. So I’m now sure that fine isn’t the best word to describe how I’m doing with all of this. I’ve got nothing to say about the election that you haven’t already thought yourself, except to re-emphasize that neither denial nor rationalization are much help on either side of this coin.

1. here’s Linus…
2. show me the damn  code  numbers!…
3. the commercial strangle-hold
4. the basic efficacy table I…
5. the basic efficacy table II…

I was on an international team that applied for and analyzed an RCT from 2001 [Restoring Study 329: efficacy and harms of paroxetine and imipramine in treatment of major depression in adolescence]. It was a herculean task – rewarding, but labor intensive and often frustrating [see https://study329.org/]. While I learned a lot, there aren’t going to be too many such studies in its current form because it requires so much effort, time, and expertise. And so full Data Transparency [which I’ve supported on this blog] is a solution for special cases, but not everyday use. It would be infinitely easier if the data were in the public domain, not captive in the remote desktop interface and subject to so many restrictions, but the pharmaceutical companies have buried their heels deep into the pavement. They’re going to any length to hold onto it.

There’s something else. These short term RCTs are done for New Drug Approvals [NDAs] or New Indication Approvals, and that may be fine for that kind of initial testing – maybe the only real way to bring off the FDA’s opener. But like the case of the SSRIs or the COX-2 inhibitors [Vioxx®, Celebrex®], people might take these drugs for months, or even years, rather than just a few weeks. And that’s what got me to thinking about the "prototypical nerd," Linus Tolvold [here’s Linus…]. He didn’t set out to challenge the commercial monopoly, but challenge it he did. And the reason I say it will ultimately come out on top is that the development of Linux is driven by the science of computing, not the profits of the enterprise.

There are some things we need to do to clean up the woefully unregulated Clinical Trial problem, sure enough. But salvation depends of our developing a system that persists past approval. The data is there. We just haven’t figured out how to harvest it and create something that grows instead of a system that seems stuck on first base. Short term trials don’t even need an article for efficacy, just a simple basic efficacy table and for adverse events – a truthful compilation of adverse events – box scores. After all, it’s just product testing. It’s what’s missing that matters…

When Dr. Bernard Carroll comments here, he often uses the term "hand waving" when describing some of the tricky maneuvers used in the clinical trial reports to smooth over shaky logic or rationalize absurdities. It’s a great term, I think originating in the world of stage magicians who use exaggerated gesticulations to distract your attention. My wife’s a figure skating fan, and there it’s called "hand dancing" – dramatic arm and hand gestures to cover up sloppy skating. After reading so many jury-rigged clinical trial reports, I’ve almost come to see the whole narrative as organized around a verbal version of these attempts at artifice, and find myself jotting down the essential pieces in a hastily sketched table on the back of a nearby envelope or piece of scrap-paper. So the basic efficacy table isn’t just a concept or a proposal. It’s an outgrowth of my experience. I guess the formula goes:

article narrative – bullshit = basic efficacy table

One thing the ghost-writers seem to count on is that most doctors look at the abstract, scan the graphs and tables, and move on. I used to see that as virtue – getting through so much material on a regular basis. In my doctor youth, I could do that. But no longer. If a Clinical Trial report or a review article is there to be read, it’s there to be read closely, pencil and envelope back at the ready. At least that’s true of the industry funded clinical trials of psychiatric drugs that I find myself reading these days.

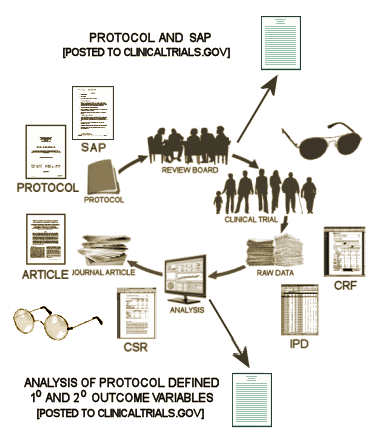
When I drew this diagram, it’s not how things are. It’s how I wish they would be. Step one is the approval of the study Protocol by the Institutional Review Board. At that point, by my reckoning, the trial should be registered [on ClinicalTrials.gov]. There’s no reason at all that the Protocol couldn’t be published at that point. It has been written down for the IRB. Why not make it a part of the registration process. That would mean that a bona fide copy of the a priori declarations would be available from the outset.

adapted from Table 1A in

Trial Reporting in ClinicalTrials.gov — The Final Rule

by Deborah A. Zarin, Tony Tse, Rebecca J. Williams, and Sarah Carr

New England Journal of Medicine. 2016 375[20]:1998-2004.

[full text on-line]

First off, anything they do is a step forward. They’ve had the machinery available for two decades, and have done little with it. So they’re finally requiring registration for all the studies, and they pledge to keep up with it. An excellent start.

Initial Registration:  They say that they want the submission of the trial registration within three weeks of the initial subject’s enrollment and posting on-line within the 30 days after submission. Of course I’d prefer our "before the study starts" timing, but within the first two months will do. The point is to get it registered before they can look at the results and modify the Protocol – and two months is early enough for me. As for what’s to be posted, they don’t require posting the whole Protocol. That’s a disappointment. I’d prefer anchoring the outcome parameter at the beginning. But at least they do require declaration of the Primary Outcome Variables with registration.

Posting the Results:  This has traditionally been the most ignored requirement. They say: "Outcomes and statistical analyses for each primary and secondary outcome measure by treatment group or comparison group, including results of scientifically appropriate statistical analyses performed on these outcomes, if any" and add in "Protocol and statistical analysis plan to be submitted at time of results information reporting (may optionally be submitted earlier)." And I say A+! With that information, I could fill out my entire basic efficacy table, The only thing they left out was the Effect Size and there would be ample information to do that calculation.

And for timing on the Results? I’d have to say "barely passing," if that. "Within 12 months after the date of final data collection for the prespecified primary outcome measures (primary completion date)" and "May be delayed for up to 2 additional years (i.e., up to 3 years total after the primary completion date) for trials certified to be undergoing commercial product development for initial FDA marketing approval or clearance or approval or clearance for a new use." That’s a disappointment, and I can’t see any reason for it. The results are just what they are – they’re the results of the prespecified variables analyzed in the prespecified way. Who needs time for that? But I’ll have to admit that if they were to actually to follow these standards, the improvement would still be dramatic, probably satisfy most of us. With new drugs or new indications, they’d still be early in the drug’s patent life.

• the a priori declared primary and secondary outcome variables
• the prospectively defined statistical analysis plan
• the values, variance, and effect size for those specific parameters

I don’t know if my musings about the Linux story worked, but what I was trying to talk about was the computer community’s struggles with the secrecy of the commercial developers – a problem similar to ours with Clinical Trials and their sponsors. Watching those computer code struggles happen from the sidelines, things took of when Linux came around and they had a new own platform [operating system]. Linus’s problem with "UI" [user interface] has held them back [see Ted talk – in here’s Linus…], but others are beginning to make it easier to use now. My point was rather than trying to gain access to the systems of others, they came into their own when they had their own system.

For many reasons, I think that something similar is ultimately the only real solution to the problem of industry’s control of drug trial and reportings. RCTs may be appropriate for drug approval purposes, the and FDA usually bases the approval on making the a priori declared primary outcome variables. But they aren’t so appropriate for deciding about actual usage of the drugs, particularly when presented in the journal articles we call experimercials – often distorted by a variety of tricky moves. Medicine is going to have to find some non-commercially driven way to test drugs that will give us reliable ongoing clinical information – our own Open Source platform.

But in the meantime, I’ve been thinking about data transparency – having access to all of the raw data from clinical trials. I certainly think that’s the way it should be. Medicine is almost by definition an open science. The majority of clinical education is apprenticeship, freely given. No secret potions, no wizards allowed. Secret data just doesn’t fit. But the business end of industry isn’t medicine. I frankly doubt that we’ll get access to all the data free and clear any time soon. It’ll probably always long be a fight like it was for us with Paxil Study 329. The marketeers see that data as part of their commodity and hold on to it at any cost. So they’ll stick with their restrictive data sharing meme as long as possible; jump on any legality they can find along the way; play havoc with the EMA’s or anyone else’s data release plan; etc. [and they can afford a lot of havoc!].

1. What are the a priori defined primary and secondary outcome variables and how will they be analyzed?
2. What are the results of those specific analyses after the study was completed?

So, whether we have access to the raw data or not, we should be able to fill out this Basic Efficacy Table [or something close] for every Clinical Trial. The reasons we can’t are mixed up with non-compliance and non-enforcement, not non-consensus or non-requirenent:

Financial ties of principal investigators and randomized controlled trial outcomes: cross sectional study

by Rosa Ahn, Alexandra Woodbridge, Ann Abraham, Susan Saba, Deborah Korenstein, Erin Madden, W John Boscardin, and Salomeh Keyhani.

BMJ 2017 356:i6770

[full text on-line]

Objective: To examine the association between the presence of individual principal investigators’ financial ties to the manufacturer of the study drug and the trial’s outcomes after accounting for source of research funding.

Design: Cross sectional study of randomized controlled trials [RCTs].

Setting: Studies published in “core clinical” journals, as identified by Medline, between 1 January 2013 and 31 December 2013.

Participants: Random sample of RCTs focused on drug efficacy.

Main outcome measure: Association between financial ties of principal investigators and study outcome.

Results: A total of 190 papers describing 195 studies met inclusion criteria. Financial ties between principal investigators and the pharmaceutical industry were present in 132 [67.7%] studies. Of 397 principal investigators, 231 [58%] had financial ties and 166 [42%] did not. Of all principal investigators, 156 [39%] reported advisor/consultancy payments, 81 [20%] reported speakers’ fees, 81 [20%] reported unspecified financial ties, 52 [13%] reported honorariums, 52 [13%] reported employee relationships, 52 [13%] reported travel fees, 41 [10%] reported stock ownership, and 20 [5%] reported having a patent related to the study drug. The prevalence of financial ties of principal investigators was 76% [103/136] among positive studies and 49% [29/59] among negative studies. In unadjusted analyses, the presence of a financial tie was associated with a positive study outcome [odds ratio 3.23, 95% confidence interval 1.7 to 6.1]. In the primary multivariate analysis, a financial tie was significantly associated with positive RCT outcome after adjustment for the study funding source [odds ratio 3.57 [1.7 to 7.7]. The secondary analysis controlled for additional RCT characteristics such as study phase, sample size, country of first authors, specialty, trial registration, study design, type of analysis, comparator, and outcome measure. These characteristics did not appreciably affect the relation between financial ties and study outcomes [odds ratio 3.37, 1.4 to 7.9].

Conclusions: Financial ties of principal investigators were independently associated with positive clinical trial results. These findings may be suggestive of bias in the evidence base.

Discussion
We found that more than half of principal investigators of RCTs of drugs had financial ties to the pharmaceutical industry and that financial ties were independently associated with positive clinical trial results even after we accounted for industry funding. These findings may raise concerns about potential bias in the evidence base.

Possible explanations for findings
The high prevalence of financial ties observed for trial investigators is not surprising and is consistent with what has been reported in the literature. One would expect industry to seek out researchers who develop expertise in their field; however, this does not explain why the presence of financial ties for principal investigators is associated with positive study outcomes. One explanation may be “publication bias.” Negative industry funded studies with financial ties may be less likely to be published. The National Institutes of Health [NIH]’s clinicaltrials.gov registry was intended to ensure the publication of all trial results, including both NIH and industry funded studies, within one year of completion. However, rates of publication of results remain low even for registered trials…

 

Other possible explanations for our findings exist. Ties between investigators and industry may influence study results by multiple mechanisms, including study design and analytic approach. If our findings are related to such factors, the potential solutions are particularly challenging. Transparency alone is not enough to regulate the effect that financial ties have on the evidence base, and disclosure may compromise it further by affecting a principal investigator’s judgment through moral licensing, which is described as “the unconscious feeling that biased evidence is justifiable because the advisee has been warned.” Social experiments have shown that bias in evidence is increased when conflict of interest is disclosed. One bold option for the medical research community may be to adopt a stance taken in fields such as engineering, architecture, accounting, and law: to restrict people with potential conflicts from involving themselves in projects in which their impartiality could be potentially impaired. However, this solution may not be plausible given the extensive relationship between drug companies and academic investigators. Other, incremental steps are also worthy of consideration. In the past, bias related to analytic approach was tackled by a requirement for independent statistical analysis of major RCTs. Independent analysis has largely been abandoned in favor of the strategy of transparency, but perhaps the time has come to reconsider this tool to reduce bias in the analysis of RCTs. This approach might be especially effective for studies that are likely to have a major effect on clinical practice or financial implications for health systems. Another strategy to reduce bias at the analytic stage may be to require the publishing of datasets. ICMJE recently proposed that the publication of datasets should be implemented as a requirement for publication. This requirement is increasingly common in other fields of inquiry such as economics. Although independent analyses at the time of publication may not be feasible for journals from a resource perspective, the requirement to release the dataset to be reviewed later if necessary may discourage some forms of analytical bias. Finally, authors should be required to include and discuss any deviations from the original protocol. This may help to prevent changes in the specified outcome at the analytic stage…

• The Randomized Controlled Trial [RCT] is a good way to determine clinical usefulness.

  In 1962, the FDA was charged with requiring two Randomized Controlled Trials [RCTs] demonstrating statistical efficacy and all human usage data demonstrating safety in order to approve a drug for use.  It’s a weak standard, designed to keep inert potions off the market. It was presumed that the medical profession would have a higher standard and determine clinical usefulness. That made [and makes] perfect sense. The FDA primarily insures safety and keeps swamp root and other patent medicines out of our pharmacopeia, but clinical usefulness should be determined by the medical profession and our patients. Not perfect, but I can’t think of a better system for approval. However, approval doesn’t necessarily correlate with clinical usefulness, or for that matter, long term safety. And then something unexpected happened. The Randomized Controlled Trials became the gold standard for everything – called Evidence Based Medicine. Randomized Clinical Trials are hardly the only form of valid evidence in medicine. That was a reform idea that kept people from shooting from the hip, but was also capable of throwing the baby out with the bathwater.

  This structured procedure designed to dial out everything and isolate the drug effect [RCTs] became a proxy for the much more complex and varied thing called real life. RTCs have small cohorts of recruited [rather than help-seeking] subjects in short-term trials. Complicatred patients are eliminated by exclusionary criteria. The metrics used are usually clinician-rated rather than subject-rated. And the outcome is measured by statistical significance instead of by the strength of the response. Blinding and the need for uniformity eliminates any iterative processes in dosing or identifying target symptoms. It’s an abnormal situation on purpose, suitable for the yes-no questions in approval, but not the for-whom information of clinical experience.

• It is ever going to be possible to create a system that insures that the industry sponsors will openly report on their RCT without exaggerrating efficacy and/or understating toxicity.

  These RCTs were designed for submission to the FDA for drug approval. The FDA reviewers have access to the raw data and have regularly made the right calls. But then those same studies are written up by professional medical ghost writers, signed onto by KOL academic physicians with florid Conflicts of Interest and submitted to medical journals to be reviewed by peer reviewers who have no access to the raw data. The journals make money from selling reprints back to to the sponsors for their reps to hand out to practicing doctors. These articles are where physicians get their information, and discrepancies between the FDA version and the Journal versions are neither discussed, nor even easy to document.

  So it’s not the FDA Approval that’s the main problem. It’s the glut of journal articles that have been crafted from those studies and been the substrate for advertising campaigns that have caused so much trouble. The basic Clinical Trials that were part of the Approval have been glamorized. And many trials that were unsuccessful attempts at indication creep have been spun into gold. It seems that every time there’s an attempt to block the fabulation of such trials, there have been countermoves that render the reform attempts impotent. So far, it’s been a chess game that never seems to get to check-mate.

Structured RCTs may well be the best method for our regulatory agencies use to evaluate new drugs. They cost a mint to do and about the only people who can fund them are the companies who can capitalize on success – the drug companies. But medicine  doesn’t need to  shouldn’t buy into the notion that they’re the only way to evaluate the effectiveness of medicinal products. As modern medicine has become increasingly organized and documented, there are huge caches of data available. And it’s not just patient data or clinic data. What about the pharmacy data that’s already being used by PHARMA to track physician’s prescribing patterns? And where are the departments of pharmacology and the schools of pharmacy in following medication efficacy and safety? or the HMOs? or the Health Plans? the VAH? What about the waiting room questionnaires? I’d much rather they ask about the medications the patient is on than being used to screen for depression. It’s really the ongoing data after a drug is in use that clinicians need anyway – more important than the RTC that gets things started.

^{Cartograms of the 2016 presidential election [with the country scaled by population rather than area]. On the left, colored by who won the county. On the right, color gradient by percentage vote in county.}

Back in the early PC days, the software developers [Microsoft, Apple, etc] wanted to own their software through and through, make the code proprietary. The nerds and hackers of the world said ‘show me the damn code‘ and the companies said ‘hell no.’ There were lawsuits, and posturing, and all manner of haggling about whether computer code was intellectual property. For users, it was a problem because every new release [of something like Microsoft Word] meant that to get the new features, you had to buy it again or pay for an upgrade. And that extended to the operating system itself [DOS, OS]. It was a monopoly.

When the World  Wide Web came along, there was a different tradition. The hardware came from the government [DARPA] and the language that made it work [HTML] came from a think tank [CERN] developed by Tim Berners-Lee for internal use. The Browser used to read the HTML was Mosaic, and later Netscape [that was free, a version of Open Source] – built and maintained by volunteers. Microsoft wanted to grab the Internet, so they gave their Browser away too [Internet Explorer]. Now Google’s Chrome has jumped onto the mix. The tradition of Netscape carried the day and the Open Source Movement took hold – Linux, MySQL, Open Office, Apache server, etc and a whole lot of other very important stuff you can’t see. So the companies held on to their proprietary code and the home computer market primarily by building user friendly interfaces [and inertia]. As Linus Torvolds implied in the Ted interview, hackers, geeks, and nerds don’t do interfaces very well – and they sure aren’t marketeers. So now there’s a mix of Open Source and Proprietary software that’s actually mutually beneficial – a loose symbiosis of sorts. Android being a prime example.

• PLOS [Public Library of Science] is a nonprofit open access scientific publishing project aimed at creating a library of open access journals and other scientific literature under an open content license. It launched its first journal, PLOS Biology, in October 2003 and publishes seven journals, as of October 2015.
• ClinicalTrials.gov is a registry and results database of publicly and privately supported clinical studies of human participants conducted around the world. Learn more About Clinical Studies … including relevant History, Policies, and Laws.
• PubMed comprises more than 26 million citations for biomedical literature from MEDLINE, life science journals, and online books. Citations may include links to full-text content from PubMed Central and publisher web sites.
• AllTrials/COMPare: All Trials Registered | All Results Reported. The COMPare project is systematically checking every trial published in the top five medical journals, to see if they have misreported their findings.
• Rxisk: No one knows a prescription drug’s side effects like the person taking it. Make your voice heard. RxISK is a free, independent drug safety website to help you weigh the benefits of any medication against its potential dangers.

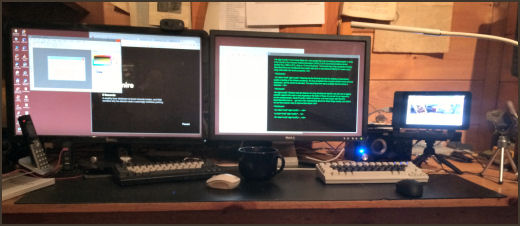
Sometimes it’s the things right under your nose that are the hardest things to see. This is my desktop at home [uncharacteristically uncluttered]. Pretty much standard fare with a couple of 27" monitors connected to a big Windows 10 computer under the desk. But there are some anomalies. Why the two keyboards? and the two mice? And what’s with that little screen on the tripod?

The screen, keyboard, and mouse on the right belong to a Raspberry Pi, a little $35 computer that runs Raspbian [a variant of the Linux Operating system – which is free], has a full range of software packages [which are free], can be programmed using the Python Language [which is downloaded free], and has a hardware interface to the outside for hackers to prototype all kind of stuff [like robots]. There’s a Raspberry Pi on the space station overhead. The Android OS that runs your phone is a variant of Linux, and the Apache software that runs almost every web server usually runs under Linux.

In the 1980s, when the personal computer burst onto the scene, you could buy programs for your computer, but they were compiled – meaning that you couldn’t see the code and you couldn’t change anything about them. The software producers essentially had a monopoly. The Open Source Movement arose on multiple fronts throughout the next few decades and is too complex to detail here, but the core idea is simple. If you buy a piece of Open Source Software, you get the compiled program AND the source code. You can do with it what you please. There are many variants but that’s the nuts and bolts of it. Linus Torvolds, a Finnish student wrote a UNIX-like operating system  [Linux] and released it Open Source [which put this movement on the map]. Netscape did the same thing. The idea is huge – that it’s fine to be able to sell your work [programs], but it’s not fine to keep the computer code under lock and key.

Before I retired, computers and programming were my hobbies, and the source of a lot of fun. I didn’t need either of them for my work [psychoanalytic psychotherapy] – they were for play. I gradually moved everything to the Linux system and Open Source. But when I retired, my first project involved georegistering old maps and projecting them onto modern topographc maps, and the only software available ran under Windows. And then with this blog, I couldn’t find an Open Source graphics program that did what I wanted. So I’ve run Windows machines now for over a decade. But I just got this little Raspberry Pi running, and I can already see that I’m getting my hobby back. If it’s not intuitive what this has to do with Randomized Clinical Trials or the Academic Medical Literature, I’ll spell it out here in a bit. But for right now – here’s Linus:

I spent a day with the article in the last post [A manifesto for reproducible science]. It lived up to my initial impression and I learned a lot from reading it. Great stuff! But my focus here is on a particular corner of this universe – the industry-funded Clinical Trial reports of drugs that have filled our medical journals for decades. And I’m not sure that this manifesto is going to add much. Here’s an example of why I say that:

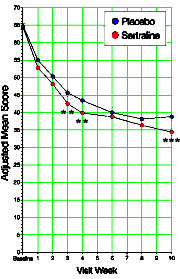Looking at one of the clinical trial articles of SSRIs in adolescents, there was something peculiar [Wagner KD. Ambrosinl P. Rynn M. et al. Efficacy of sertraline in the treatment of children and adolescents with major depressive disorder, two randomized controlled trials. JAMA. 2003;290:1033-1041.]. What does it mean "two randomized controlled trials"? Well it seems that there were two identical studies that were pooled for this analysis. Why? They didn’t say… The study was published in August 2003, and there were several letters along the way asking about this pooling of two studies. Then in April 2004, there was this letter: To the Editor: Dr Wagner and colleagues reported that sertraline was more effective than placebo for treating children with major depressive disorder and that it had few adverse effects. As one of the study group investigators in this trial, I am concerned about the way the authors pooled the data from 2 trials, a concern that was raised by previous letters critiquing this study. The pooled data from these 2 trials found a statistically marginal effect of medication that seems unlikely to be clinically meaningful in terms of risk and benefit balance. New information about these trials has since become available. The recent review of pediatric antidepressant trials by a British regulatory agency includes the separate analysis of these 2 trials. This analysis found that the 2 individual trials, each of a good size [almost 190 patients], did not demonstrate the effectiveness of sertraline in treating major depressive disorder in children and adolescents. E.Jane Garland, MD, PRC PC Department of Psychiatry University of British Columbia Vancouver So the reason they pooled the data from the two studies appears to be that neither was significant on its own, but pooling them overpowered the trial and produced a statistically significant outcome [see power calculation below]. Looking at the graph, you can see how slim the pickings were – significant only in weeks 3, 4, and 10. And that bit of deceit is not my total point here. Add in how Dr. Wagner replied to Dr. Garland’s letter: In Reply: In response to Dr Garland, our combined analysis was defined a priori, well before the last participant was entered into the study and before the study was unblinded. The decision to present the combined analysis as a primary analysis and study report was made based on considerations involving use of the Children’s Depression Rating Scale [CDRS] in a multicenter study. Prior to initiation of the 2 pediatric studies, the only experience with this scale in a study of selective serotonin reuptake inhibitors was in a single-center trial. It was unclear how the results using this scale in a smaller study could inform the power evaluation of the sample size for the 2 multicenter trials. The combined analysis reported in our article, therefore, represents a prospectively defined analysis of the overall study population… This definition ["well before the last participant was entered into the study and before the study was unblinded"] is not what a priori means. It means "before the study is ever even started in the first place." And that’s not what prospective means either. It also means "before the study is ever even started in the first place" too. She is rationalizing the change by redefining a priori’s meaning. The problem here wasn’t that Pfizer, maker of Zoloft, didn’t have people around who knew the ways of science. If anything, it was the opposite problem. They had or hired people who knew those science ways well enough to manipulate them to the company’s advantage. Why did they have two identical studies? Best guess is that they were going for FDA Approval, and in a hurry. You need two positive studies for FDA Approval. Why would they decide to pool them somewhere along the way? Best guess is that things weren’t going well and pooling them increases the chance of achieving significance with a smaller difference between drug and placebo. How would they know that things weren’t going well if the study was blinded? You figure it out. It isn’t that hard. Why would they say that a priori means "well before the last participant was entered into the study and before the study was unblinded" when that’s not what it means? That isn’t that hard to figure out either. So why not just say that they cheated? Because I can’t prove it [plausible deniability]

Child Psychiatrists Look at Specialty From Both Macro, Micro Perspectives

PsychiatricNews

by Aaron Levin

June 16, 2016

… As for treatment, only two drugs are approved for use in youth by the Food and Drug Administration [FDA]: fluoxetine for ages 8 to 17 and escitalopram for ages 12 to 17, said Wagner. “The youngest age in the clinical trials determines the lower end of the approved age range. So what do you do if an 11-year-old doesn’t respond to fluoxetine?” One looks at other trials, she said, even if the FDA has not approved the drugs for pediatric use. For instance, one clinical trial found positive results for citalopram in ages 7 to 17, while two pooled trials of sertraline did so for ages 6 to 17.

Another issue with pediatric clinical trials is that 61 percent of youth respond to the drugs, but 50 percent respond to placebo, compared with 30 percent among adults, making it hard to separate effects. When parents express anxiety about using SSRIs and ask for psychotherapy, Wagner explains that cognitive-behavioral therapy [CBT] takes time to work and that a faster response can be obtained by combining an antidepressant with CBT. CBT can teach social skills and problem-solving techniques as well. Wagner counsels patience once an SSRI is prescribed.

A 36-week trial of a drug is too brief, she said. “The clock starts when the child is well, usually around six months. Go for one year and then taper off to observe the effect.” Wagner suggested using an algorithm to plot treatment, beginning with an SSRI, then trying an alternative SSRI if that doesn’t work, then switching to a different class of antidepressants, and finally trying newer drugs. “We need to become much more systematic in treating depression,” she concluded.